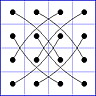
(S01) Die Menge T17 = {1,2,3,4,5,6,7,8,10,11,12,13,14,15,16,17} erlaubt 260 reduzierte GMS, somit 32*260=8320 GMS insgesamt
(vergleiche mit klassischen magischen Quadraten).
Es ist eine alte Vermutung (siehe Referenzen unten), dass diese Anzahl nicht übertroffen werden kann.
Die Vermutung ist anscheinend bis heute ebenso ungeklärt wie die Frage, ob noch andere Vektoren als die 154 genannten existieren.
Es gibt symmetrische Mengen, die gleich viele GMS erlauben, wie es klassische magische 4x4 Quadrate gibt, nämlich 7040.
Jedoch kann sich die Struktur dieser GMS ziemlich von der Struktur klassischer magischer
4x4 Quadrate unterscheiden.
(siehe Vectors154.pdf).
|
| u |
v
| |
p | o | n |
m |
l | k | j |
i |
h | g | f |
e |
d | c | b |
a |
| a |
x | |
| z |
| x |
w | y |
| w |
x | y |
z | y |
y | |
| b |
| x |
z | |
x | |
y | w |
w | |
y | x |
y | z |
| y |
| c |
| z |
x | |
w | y |
| x |
x | y |
| w |
y | |
z | y |
| d |
z | |
| x |
y | w |
x | |
y | x |
w | |
| y |
y | z |
| e |
| x |
w | y |
x | |
| z |
z | y |
y | |
| w |
x | y |
| f |
x | |
y | w |
| x |
z | |
y | z |
| y |
w | |
y | x |
| g |
w | y |
| x |
| z |
x | |
y | |
z | y |
x | y |
| w |
| h |
y | w |
x | |
z | |
| x |
| y |
y | z |
y | x |
w | |
| i |
| w |
x | y |
z | y |
y | |
x | |
| z |
| x |
w | y |
| j |
w | |
y | x |
y | z |
| y |
| x |
z | |
x | |
y | w |
| k |
x | y |
| w |
y | |
z | y |
| z |
x | |
w | y |
| x |
| l |
y | x |
w | |
| y |
y | z |
z | |
| x |
y | w |
x | |
| m |
z | y |
y | |
| w |
x | y |
| x |
w | y |
x | |
| z |
| n |
y | z |
| y |
w | |
y | x |
x | |
y | w |
| x |
z | |
| o |
y | |
z | y |
x | y |
| w |
w | y |
| x |
| z |
x | |
| p |
| y |
y | z |
y | x |
w | |
y | w |
x | |
z | |
| x |
| |
T17:
Anzahl
magischer
4x4 Quadrate
mit
u + v = 18
|
|
0 Quadrate |
| 32 Quadrate |
| 384 Quadrate |
| 608 Quadrate |
| 2336 Quadrate |
|
|
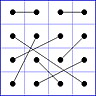 Beobachtung 2 Für jedes GMS mit kleinstem Eintrag 1 und größtem Eintrag N beträgt die magische Summe 2(N+1).
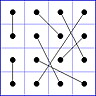
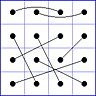
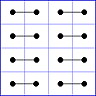
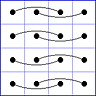
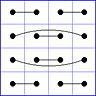
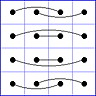
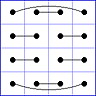
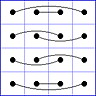
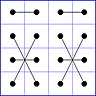
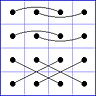
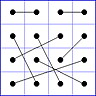
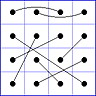
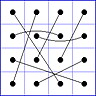
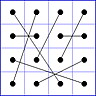
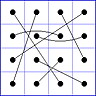
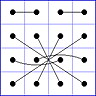
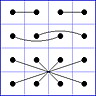
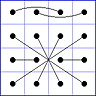
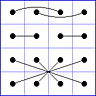
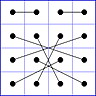
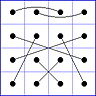
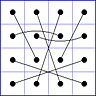
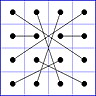
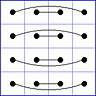
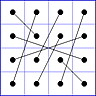
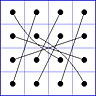
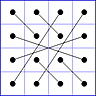
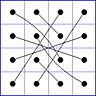
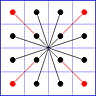
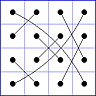
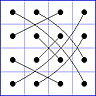
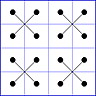
Es gibt 8 Paare von Einträgen mit Summe N+1. Werden die beiden Einträge eines solchen Paares im Quadrat durch eine Linie verbunden, so entsteht die
"Verbindungsfigur", engl.: connection figure (CF) des betreffenden magischen Quadrats (das Bild zeigt die CF für das obige GMS Beispiel).
Eine CF kann stets durch eine horizontale Zeichenkette mit 16 Einträgen beschrieben werden, z.B.
Beobachtung 2 Für jedes GMS mit kleinstem Eintrag 1 und größtem Eintrag N beträgt die magische Summe 2(N+1).
Es gibt 8 Paare von Einträgen mit Summe N+1. Werden die beiden Einträge eines solchen Paares im Quadrat durch eine Linie verbunden, so entsteht die
"Verbindungsfigur", engl.: connection figure (CF) des betreffenden magischen Quadrats (das Bild zeigt die CF für das obige GMS Beispiel).
Eine CF kann stets durch eine horizontale Zeichenkette mit 16 Einträgen beschrieben werden, z.B.