(S01) The set T17={1,2,3,4,5,6,7,8,10,11,12,13,14,15,16,17} allows 260 reduced GMS, therefore 32*260=8320 GMS (compare with classical magic squares).
That this number cannot be surpassed, is an old conjecture (see references below) and til today scientifically unproved, as well as the question whether there are other vectors than the named 154 ones .
There are symmetric sets, which allow as many GMS, as there are classical 4x4 magic squares, namely 7040. But the structure of these GMS can be rather different from the structure of classical magic squares
(see Vectors154.pdf).
|
| u |
v
| |
p | o | n |
m |
l | k | j |
i |
h | g | f |
e |
d | c | b |
a |
| a |
x | |
| z |
| x |
w | y |
| w |
x | y |
z | y |
y | |
| b |
| x |
z | |
x | |
y | w |
w | |
y | x |
y | z |
| y |
| c |
| z |
x | |
w | y |
| x |
x | y |
| w |
y | |
z | y |
| d |
z | |
| x |
y | w |
x | |
y | x |
w | |
| y |
y | z |
| e |
| x |
w | y |
x | |
| z |
z | y |
y | |
| w |
x | y |
| f |
x | |
y | w |
| x |
z | |
y | z |
| y |
w | |
y | x |
| g |
w | y |
| x |
| z |
x | |
y | |
z | y |
x | y |
| w |
| h |
y | w |
x | |
z | |
| x |
| y |
y | z |
y | x |
w | |
| i |
| w |
x | y |
z | y |
y | |
x | |
| z |
| x |
w | y |
| j |
w | |
y | x |
y | z |
| y |
| x |
z | |
x | |
y | w |
| k |
x | y |
| w |
y | |
z | y |
| z |
x | |
w | y |
| x |
| l |
y | x |
w | |
| y |
y | z |
z | |
| x |
y | w |
x | |
| m |
z | y |
y | |
| w |
x | y |
| x |
w | y |
x | |
| z |
| n |
y | z |
| y |
w | |
y | x |
x | |
y | w |
| x |
z | |
| o |
y | |
z | y |
x | y |
| w |
w | y |
| x |
| z |
x | |
| p |
| y |
y | z |
y | x |
w | |
y | w |
x | |
z | |
| x |
| |
T17:
number of
4x4 magic
squares
with
u + v = 18
|
|
0 squares |
| 32 squares |
| 384 squares |
| 608 squares |
| 2336 squares |
|
|
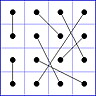
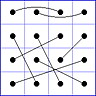
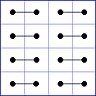
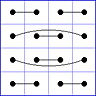
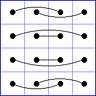
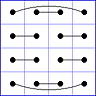
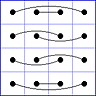
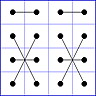
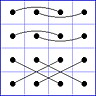
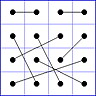
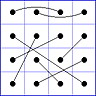
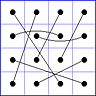
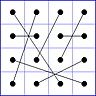
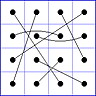
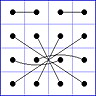
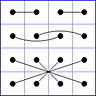
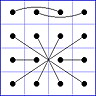
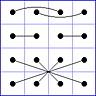
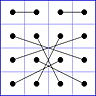
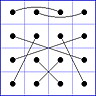
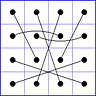
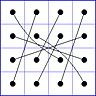
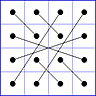
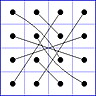
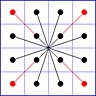
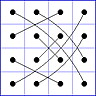
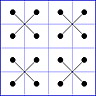
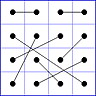 Observation 2 For any general 4x4 magic square with entries from a symmetric set, containing 1, with greatest
element N, the magic sum ist 2N+2. There are 8 pairs of entries with sum N+1. When the two entries of each such pair in the square are connected
by a line, then the
connection figure (CF) of the square is generated (here the connection figure of the above example GMS
is shown). Any CF can be written as horizontal string with 16 entries, f.i. write
Observation 2 For any general 4x4 magic square with entries from a symmetric set, containing 1, with greatest
element N, the magic sum ist 2N+2. There are 8 pairs of entries with sum N+1. When the two entries of each such pair in the square are connected
by a line, then the
connection figure (CF) of the square is generated (here the connection figure of the above example GMS
is shown). Any CF can be written as horizontal string with 16 entries, f.i. write