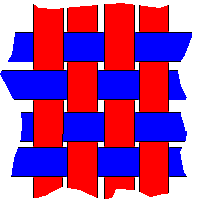
 | 

 Polyhedra plaited with paper strips | 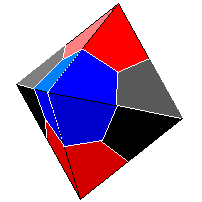 |
| Geometric Solids (Polyhedra) can be constructed by plaiting
folded paper strips without use of glue. Every strip is a sequence of certain quadrilaterals, and every folding-line is an edge or a diagonal of a quadrilateral. The plaiting considered here shall be ruled by a "Plaiting Principle": |
| 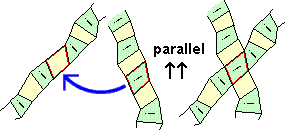 | |
| An inner quadrilateral and an outer quadrilateral can be brought onto each other "parallel" (↑↑) or "antiparallel" (↑↓). | ||
| a detailed example | a small exhibition | plaiting-scheme analysis |
|
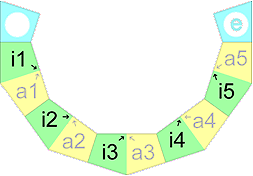
Ways of plaiting: 1. Every outer quadrilateral of a strip covers one or two sides of the polyhedron ("plain plaiting"). 2. The border of a strip always connects a certain inner point ("midpoint") of a polyhedron-side and the midpoint of a certain edge of this side. ("edge plaiting"). 3. The border of a strip always connects a certain inner point ("midpoint") of a polyhedron-side and a vertex of this side. ("vertex plaiting"). Tetrahedron, cube, octahedron, and icosahedron, for instance, can be plaited in every way, mixed forms are also possible (see: Cuboctahedron). Requirements for plaiting strips: 1. The plaiting strips of a polyhedron should be congruent to each other, if possible ("congruence property"). 2. Every plaiting strip should generate a "closed sequence of sides" of the polyhedron surface. That means: when plaiting is finished, the first edge of the first inner quadrilateral i 1 lies upon the last edge of the last outer quadrilateral of the strip. ("closedness"). 3. A plaiting strip should be "consecutive", that means containing no quadrilaterals, with 2 neighbour edges belonging to the border of the strip. 4. the plaiting strips should have the ("maximum property"), that means they should not arise from cutting bigger strips of the same polyhedron into smaller ones (see edge plaiting of the cube e. g.). |
| Platonic solids and their paper strips for plaiting: | |||
| Tetrahedron platonic Solid 4 vertices 6 edges 4 sides 4 equi- lateral triangles (4 tr.) | 
also see here |
plain 2 strips, mirror- images 2 x 2 tr. | 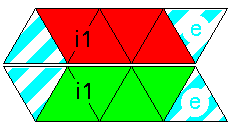 pattern download: 1060 x 620 pix, 18 kb: tg.gif or as pdf: tg.pdf |
 | edge 4 strips 3 x 2/3 tr. | 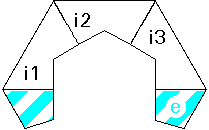 pattern download: 1350 x 780 pix, 98 kb: tt.gif or as pdf: tt.pdf | |
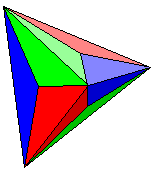 | vertex 3 strips 4 x 2/3 tr. | 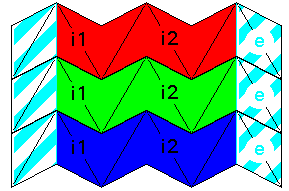 pattern download: 2593 x 1761 pix, 705 kb: tk.gif or as pdf: tk.pdf | |
| a tetrahedron plaiting with only one paper strip (mixed plain/vertex) can be found here | |||
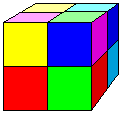
| Hexahedron (cube) platonic solid 8 vertices 12 edges 6 sides 6 squares (6 sq.) | 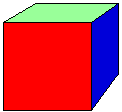 | plain 3 strips 4 sq. | 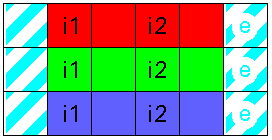 |
 | edge 6 strips 4 x 1/2 sq. |  | |
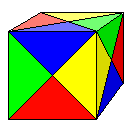 | vertex 4 strips 5 x 1/2 sq. 2 x 1/4 sq. | 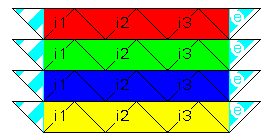
pattern download: 2801 x 1745 pix, 114 kb: str4.gif or as pdf: str4.pdf. Easy version: he4.gif or he4.pdf |
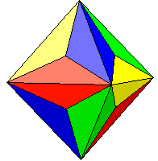
| Octahedron platonic solid 6 vertices 12 edges 8 sides 8 equi- lateral triangles (8 tr.) | 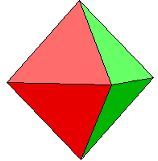 also see: here | plain 2 strips 4 x 2 tr. | 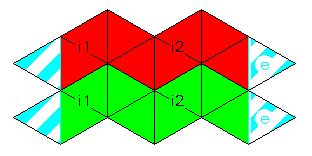 pattern download: 2100 x 1000 pix, 36 kb: og.gif or as pdf: og.pdf |
 Pseudoglobe [Carlos A. Furuti] | plain 2 strips 4 x 2 tr. | 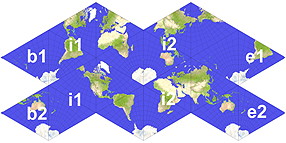 pattern download: 2800 x 1637 pix, 510 kb: oer.gif or as pdf: oer.pdf | |
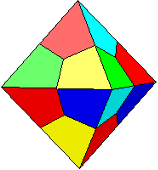 | edge 6 strips 4 x 2/3 tr. | 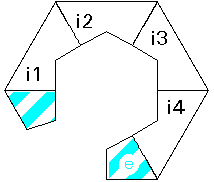
pattern download: 1500 x 1040 pix, 60 kb: ok.gif or as pdf: ok.pdf | |
 | vertex 4 strips 6 x 2/3 tr. |
 pattern download: 1620 x 1160 pix, 54 kb: oe.gif or as pdf: oe.pdf | |
| a plain plaiting of the octahedron with only one paper strip can be found here | |||
|
Dodeca- hedron platonic solid 20 vertices 30 edges 12 sides 12 regular pentagons (12 pe.) | 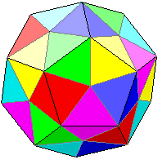 plaiting instructions | vertex 6 strips 10 x 2/5 pe. |
a detailed guide to the vertex-plaiting of the dodecahedron is also given here (in German language). pattern download: 2340 x 1370 pix, 74 kb: de.gif or as pdf: de.pdf |
 | egde 12 strips 5 x 2/5 pe. |
 pattern download: 2655 x 1971 pix, 88 kb: dk2.gif or as pdf: dk2.pdf | |
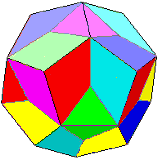 | vertex 6 strips 10 x 2/5 pe. | 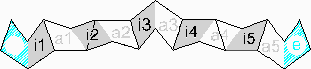 pattern download: 3249 x 2750 pix, 233 kB: dv.gif or as pdf: dv.pdf | |
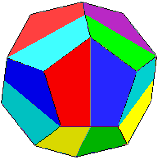 | mixed edge/vertex 6 strips 8 x 1/2 pe. | 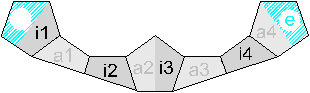 pattern download: 2889 x 2032 pix, 125 kB: doh.gif or as pdf: doh.pdf | |
nice spiral: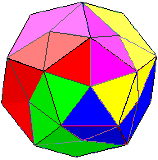 plaiting instruction: 1) i16↑↑a3 2) i4↑↑a21, i21↓↑a16 3) i22↑↑a9, i9↓↑a4, i17↑↑a8 4) i10↑↑a27, i28↑↑a15, .. |
vertex 1 strip (divided into 5 parts) 60 x 2/5 pe. (12 x 2/5 pe. per part) | 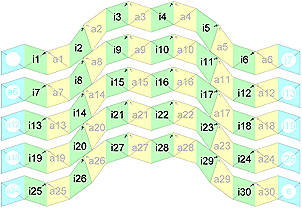 pattern download: 3213 x 2200 pix, 236 kb: sr5.gif or as pdf: sr5.pdf |
|
Icosahedron platonic solid 12 vertices 30 edges 20 sides 20 equi- lateral triangles (20 tr.) |
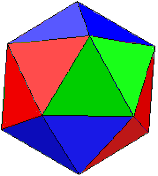 | plain 1 strip (divided into 3 parts) 20 x 2 tr. | 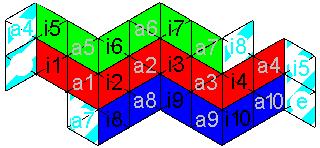 plaiting instruction: i3↓↑a6, i6↑↑a9, i9↓↑a2, i2↑↑a5, i10↑↑a3, i7↓↑a10, i5↓↑a8, i4↑↑a7, i8↑↑a1, and i1↓↑a4. representation as knot pattern download: 2950 x 1480 pix, 217 kb: ivn.gif or as pdf: ivn.pdf |
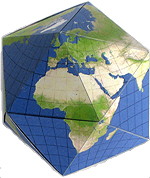 Pseudoglobe | plain 1 strip (divided into 5 parts) 20 x 2 tr. |  pattern as pdf-file: icoerde.pdf | |
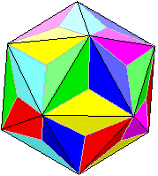 plaiting instructions | vertex 6 strips 10 x 2/3 tr. |  pattern download: 2400 x 1560 pix, 98 kb: ic.gif or as pdf: ic.pdf | |
 | edges 12 strips 5 x 2/3 tr. |
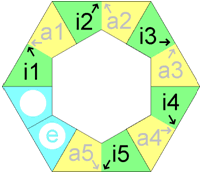 pattern download: 1800 x 1050 pix, 65 kB: ik6.gif or as pdf: ik6.pdf | |
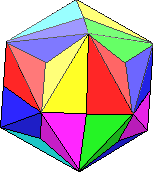 | mixed edge/vertex 6 strips 4 x 2/3 tr. 6 x 1/2 tr. 1 tr. | 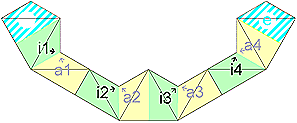 pattern download: 1305 x 2017 pix, 120 kB: st6.gif or as pdf: st6.pdf |