| An Example: (Deltoidal Icositetrahedron) | |||
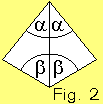
| A triangle with angles fulfilling the given conditions (Fig. 1) is reflected at its long edge (Fig. 2). From the resulting mirror-symmetric quadrilateral (Fig. 3) a strip consisting of 8 mirror-symmetric quadrilaterals, which are congruent, is generated by multiple reflection. (Fig. 4). | 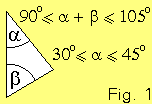 |
 |  |
 |
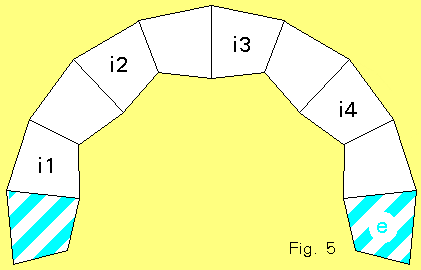
A paper strip for plaiting is completed by appending two additional mirror-symmetric quadrilaterals (marked blue), for the purpose of fastening the strip finally. The 4 inner quadrilaterals of the strip are marked i 1 to i 4 (Fig. 5). When the plaiting is done later, the quadrilateral marked "e" (end) of the strip always will finally be fixed under another strip. The strip must be folded along the edges of the quadrilaterals (9 foldings), always in the same direction (i.e. no zigzag). |
 |
In order to produce the plaited polyhedron serving as an example, 6 folded paper strips First of all, the strips one by one have to be brought into the position shown in Fig. 6. The strips may temporarily be fixed together with e.g. paper clips. |
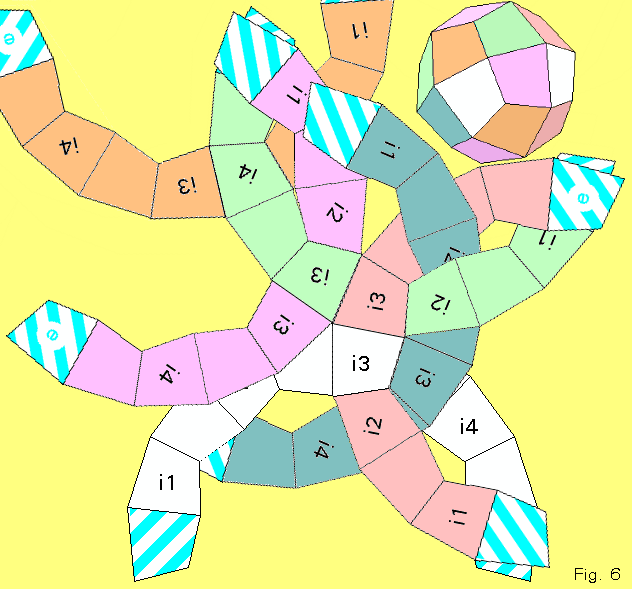 |
Now the strips are plaited together. The Plaiting Principle has to be observed: 1. Every inner quadrilateral of each strip must lie on a certain outer quadrilateral of another strip. 2. For every strip inner and outer quadrilaterals alternate with each other. As a result a polyhedron (a generalized Deltoidal Icosi- tetrahedron) shown in Fig. 6 arises. |
| special cases: with angles alpha = 30o and beta = 60o an octahedron arises, with alpha = beta = 45o a hexahedron (cube) is plaited. |