Beobachtungen über magische 4x4 Flächen-Quadrate mit vertikalen Linien
© H.B. Meyer         klassische magische 4x4 Quadrate         Kerne magischer Quadrate         magische Quadrate und Würfel         page in English language

28 26 24 22 13 21 29 37 40 30 20 10 19 23 27 31

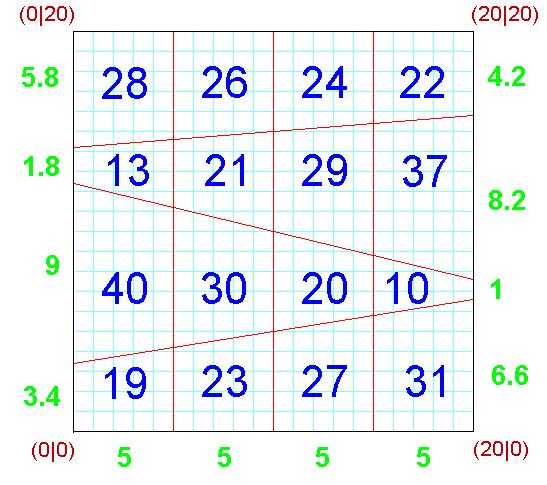
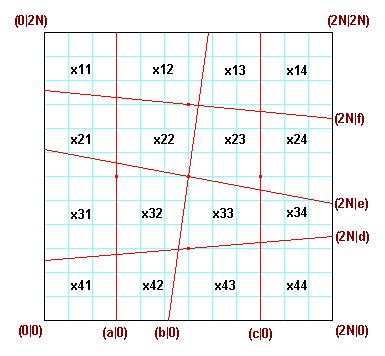
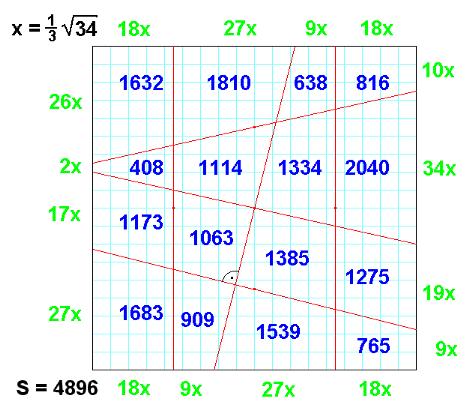
ist ein magisches 4x4 Flächen-Quadrat mit 3 vertikalen Linien (VL-AMS, "vertical line area magic square"):  - die 16 Einträge sind verschiedene natürliche Zahlen,  - die 4 Zeilen-, die 4 Spalten- und die 2 Diagonalensummen ergeben das gleiche Resultat (=100).  - es gibt ein geometrisches Quadrat (hier mit der Seitenlänge 20), das durch 3 vertikale Geraden und 3 schräg verlaufende Geraden so    in 16 Trapeze eingeteilt wird, dass jeder Eintrag des VL-AMS gerade den Flächeninhalt des zugehörigen Trapezes wiedergibt.

Die Menge T={10,13,19,20,21,22,23,24,26,27,28,29,30,31,37,40} der Einträge ist eine symmetrische Menge, d.h.: für jedes x aus T gehört die Zahl N+a-x ebenfalls zu T; hierbei bedeutet N=40 die größte und a=10 die kleinste Zahl in T.

Ziel dieser Webseite   Es werden 4x4 VL-AMS betrachtet. Welche und wie viele VL-AMS gibt es, und welche Struktur haben sie und die Mengen ihrer Einträge.

Bemerkung  Das Konzept der VL-AMS geht auf eine Idee von William Walkington zurück; das erste VL-AMS (in einer um 90 Grad gedrehten Form) wurde von Walter Trump angegeben, dem viele der hier angestellten Überlegungen zu verdanken sind.

Beobachtung 1   Wenn q die Seitenlänge des zu einem VL-AMS gehörenden geometrischen Quadrats ist, dessen linke untere Ecke im Ursprung (0|0) liegt, dann verlaufen die 3 nicht-vertikalen Trennungsgeraden durch die Punkte (q/2|3q/4) bzw. (q/2|q/2) bzw. (q/2|q/4).
In jeder Zeile des VL-AMS haben benachbarte Einträge die gleiche Differenz.

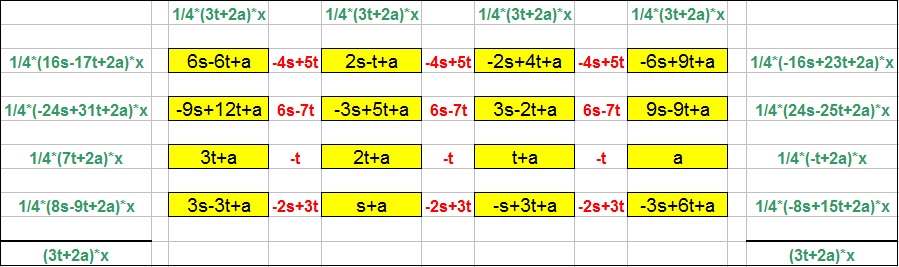
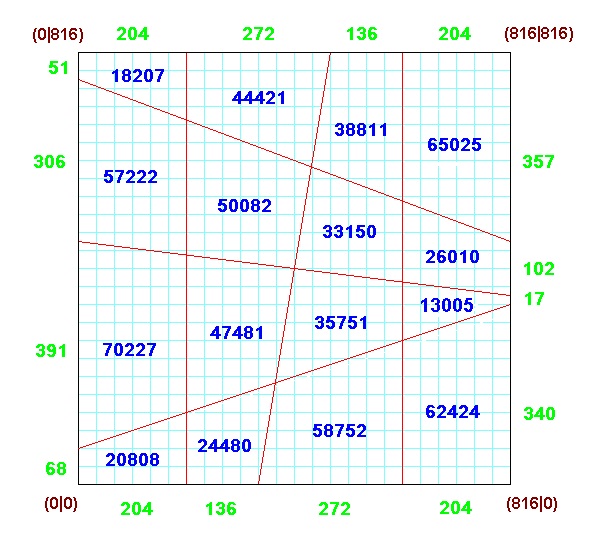
Beobachtung 2   Für jedes VL-AMS mit kleinstem Eintrag a und größtem Eintrag N beträgt die magische Summe 2(N+a). Es gibt 8 Paare von Einträgen mit Summe N+a. Werden die beiden Einträge eines solchen Paares im Quadrat durch eine Linie verbunden, so entsteht die "Verbindungsfigur" des VL-AMS. Man sagt: das VL-AMS ist ein magisches Quadrat vom Dudeney Typ VI. Wird ein VL-AMS an einer Mittellinie horizontal oder vertikal gespiegelt oder wird es um 180 Grad gedreht, so entsteht wieder ein VL-AMS.

Beobachtung 3  Jedes VL-AMS lässt sich durch 3 Parameter s,t und a wie folgt beschreiben:
Die gelb unterlegten Terme sind die Einträge des VL-AMS, die roten Terme stellen die Differenzen zeilenweise benachbarter Einträge dar und die grünen Terme bedeuten die Trapezseitenlängen an den Rändern des geometrischen Quadrats. Diese Parametrisierung lässt sich mittels Linearer Algebra unschwer beweisen.
Die Seitenlänge des geometrischen Quadrats ist q = (3t+2a)*x, mit der Einheitsgitterlänge x = √(8/(3t+2a)). Die magische Summe beträgt S = 6t+4a, somit q = 2*√S. Wenn S eine Quadratzahl ist, dann sind alle Seitenlängen der 16 Trapeze rationale Zahlen.
Die Steigungen der 3 nicht-vertikalen Trennungsgeraden sind m₁ = (8s-10t)/(3t+2a), m₂ = (-4s+4t)/(3t+2a) und m₃ = (-4s+6t)/(3t+2a) mit m₁ + m₂ + m₃ = 0. Im obigen Beispiel ist s=13, t=10, a=10.

Beobachtung 4  Durch Vergleich des Eintrags 6s-6t+a mit 3s-3t+a und mit 9s-9t+a ergibt sich, dass 6s-6t+a nicht der kleinste Eintrag des VL-AMS sein kann. Wegen der Möglichkeit von Drehungen und Spiegelungen kann der kleinste Eintrag nicht in einer Ecke liegen. Somit kann man stets annehmen, dass a der kleinste Eintrag ist, und dann N=3t+a der größte Eintrag.

Beobachtung 5  Die Einträge des VL-AMS sowie die Trapezseitenlängen (grün) müssen positiv sein, dies erfordert die Bedingungen: 0 < t < s < 4/3*t < 8/3*a.
Beobachtung 6  Die gelb unterlegten Einträge in der obigen Parametrisierung müssen paarweise verschieden sein, dies wird garantiert durch die Bedingungen n*s ≠ (n+1)*t für n = 4,5,6,7,8,9 und n*s ≠ (n+2)*t für n = 7,9,11.
Beobachtung 7  Wird zu jedem Eintrag eines VL-AMS die Zahl 1 addiert, so entsteht wieder ein VL-AMS, ebenso, wenn jeder Eintrag mit einer positiven Zahl r multipliziert wird.
Eine lineare Transfomation VL-AMS₂ = r * VL-AMS₁ + b mit ganzzahligen r,b führt ein VL-AMS₁ über in ein VL-AMS₂.
Ein VL-MS heißt fundamental, wenn es nicht durch eine solche Transformation aus einem anderen VL-AMS hervorgeht. Es gibt 720 VL-AMS mit magischer Summe ≤ 200, unter ihnen 50 fundamentale VL-AMS.
Eine Excel-Datei mit diesen genannten VL-AMS findet sich hier, die Einträge sind zeilenweise von oben links nach unten rechts zu lesen. Die kleinstmögliche magische Summe ist 84 und der kleinstmögliche Eintrag eines VL-AMS ist die Zahl 6.

Beobachtung 8  Es existieren auch lineare magische 4x4 Flächenquadrate mit nur 2 vertikalen Linien ("V2L-AMS"): Dieses Beispiel mit magischer Summe 816²/4 ist ebenfalls ein magisches Quadrat vom Dudeney Typ VI; hier sind alle dargestellten Zahlen Vielfache von 17. Es wurde gefunden mit einer Suche nach natürlichen Zahlen b,d,e,f, b≠N, auf einem 2N x 2N Gitter derart, dass die x₁₁,x₁₂,....x₄₄ zunächst ein magisches Quadrat mit rationalen Einträgen darstellen.
Danach wurden der Hauptnenner HN der Einträge x₁₁,x₁₂,...,x₄₄ bestimmt und diese mit HN² multipliziert. Mittels Spiegelungen oder 180°-Drehung kann b<N und d+N≤f erreicht werden. Eine Excel-Datei mit solchen Quadraten für N=24 bis N=96 findet sich hier, die (bereits mit HN² multiplizierten) Einträge sind als Viererzeilen von links oben nach rechts unten zu setzen.
Wenn ein magisches 4x4-Flächenquadrat mit 2 Vertikalen und Einträgen x₁₁,x₁₂,....x₄₄ gegeben ist, lassen sich die Zahlen d, e und f leicht berechnen, z.B.: d = (14x₄₄-2x₄₁)/(6N) Die Zahl b ergibt sich als b = N/2 + (-x₁₁+12x₁₃-5x₁₄-x₂₁+12x₂₃-5x₂₄)/(6N).
Es gibt sogar V2L-AMS' bei denen die Linie durch (b|0) und die Linie durch (2N|d) orthogonal sind, dies ist der Fall, wenn 2b-2d = N gilt.
Hierzu ein Beispiel, abgeleitet aus N=36, b=27, d=9, e=28, and f=62:
Verweise (englische Seiten)

William Walkington:	Area Magic Squares of Order-4
	Area Magic Squares of Order-6
Walter Trump:	Area Magic squares

Letzte Aktualisierung: 20. Oktober 2018