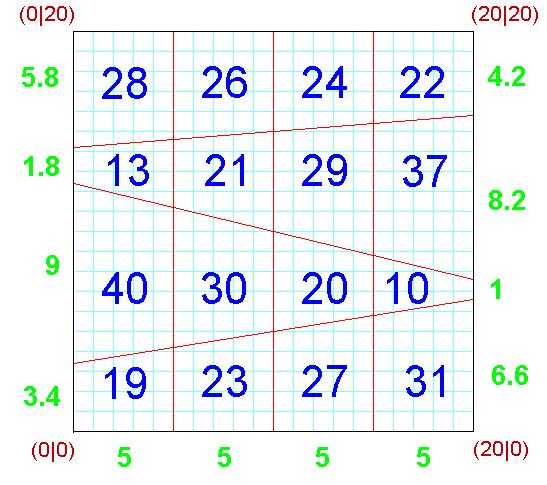
|
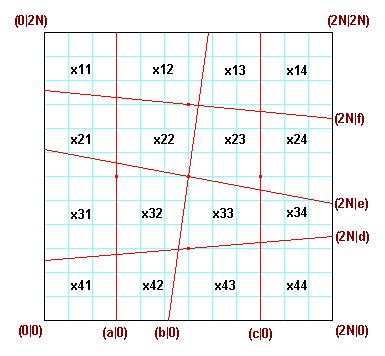
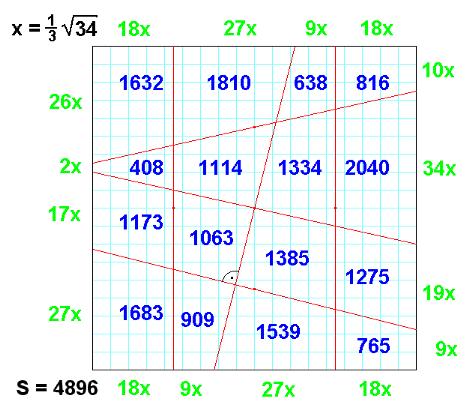
is a 4x4 Area Magic Square with Vertical Lines (VL-AMS): - the 16 entries are different natural numbers, - the 4 rows, the 4 columns and the 2 diagonals sum up to the same result (=100). - there exists a geometric square (with side length 20 here), which can be divided into 16 trapezoids by 3 vertical and 3 skew straight lines, such that every VL-AMS entry is exactly the area of the corresponding trapezoid. |

|
Observation 2 For every VL-AMS with smallest entry a und greatest entry N the magic sum is 2(N+a).
There are 8 pairs of entries with sum N+a. If both entries of such a pair are connected by a line, then the "connection figure" of the
VL-AMS is formed: the VL-AMS is a magic square of Dudeney Typ VI. Reflection at a vertical or horizontal central line or a 180 degree rotation of any VL-AMS results to a VL-AMS again. |  |
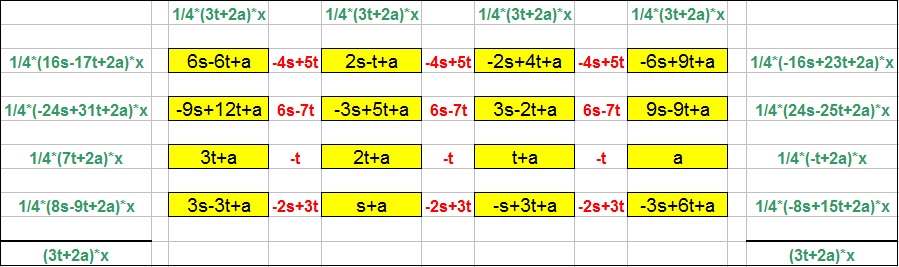
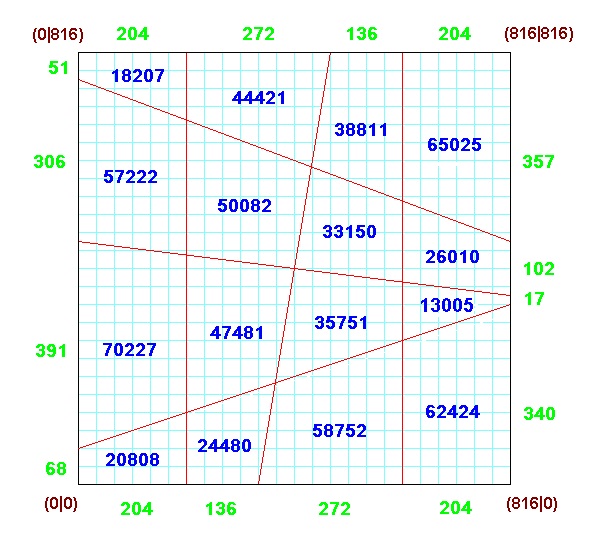 |  |
| William Walkington: | Area Magic Squares of Order-4 |
| Area Magic Squares of Order-6 | |
| Walter Trump: | Area Magic squares |