Flechtschema

Analyse eines Flecht-Schemas

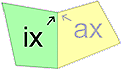Gegeben sei ein Satz von 6 kongruenten Flechtstreifen I, II, III, IV, V, und VI mit je 4 Außenvierecken a1, a2, a3, a4 und 4 Innenvierecken i1, i2, i3, i4. Innen- und Außenvierecke wechseln sich jeweils ab, jeder Streifen beginnt mit dem Innenviereck i1. Alle benachbarten Vierecke ix und ax werden mit der abgebildeten Orientierung versehen. Die Streifen werden nach folgendem Schema verflochten:

	a1	a2	a3	a4
I	↑↑ i3 IV	↑↑ i2 II	↑↑ i1 III	↑↑ i4 VI
II	↑↑ i1 V	↑↑ i2 III	↑↑ i1 I	↑↑ i2 IV
III	↑↑ i1 VI	↑↑ i2 I	↑↑ i1 II	↑↑ i4 V
IV	↑↑ i3 VI	↑↑ i2 V	↑↑ i3 II	↑↑ i4 I
V	↑↑ i3 III	↑↑ i4 II	↑↑ i1 IV	↑↑ i2 VI
VI	↑↑ i3 I	↑↑ i4 III	↑↑ i3 V	↑↑ i4 IV

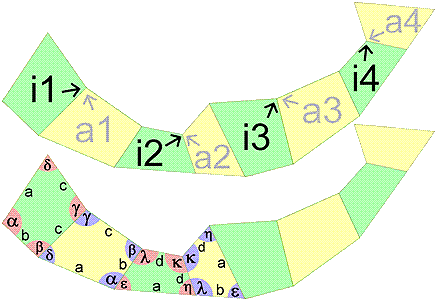Dabei bedeutet z.B. a2 III ↑↑ i2 I, dass beim Flechten das Innenviereck i2 des Streifens I so auf das Außenviereck des Streifens III zu bringen ist, dass die Orientierungspfeile beider Vierecke gleich gerichtet sind.
Aus Bedingung, dass die Flechtstreifen paarweise kongruent sein sollen und aus der der Tabelle ergibt sich, dass es zwei Klassen gleichsinnig kongruenter Vierecke auf den Streifen gibt: {i1, i3, a1, a3} und {i2, i4, a2 a4}. Ein einzelner Flechtstreifen hat deshalb folgendes Aussehen:

Die Längen a, b, c und d sowie die Winkel α, β, γ, δ, ε, η, κ und λ müssen innerhalb gewisser Grenzen gewählt werden. Insbesondere sind die nachstehenden Winkelbedingungen:
γ ≤ 120^o,
κ ≤ 120^o,
β + δ + η + λ ≤ 360^o,
α + ε ≤ 180^ozu erfüllen. Sie ergeben sich daraus, dass beim Verflechten der Streifen bestimmte Winkel jeweils in einer Ecke des Flechtkörpers zusammentreffen, deren Winkelsumme 360^o nicht überschreiten kann. Der entstehende Flechtkörper hat nämlich 26 Punkte ("Ecken"), in denen die angegebenen Winkel zusammentreffen:

1: α(a1 I), ε(a2 IV), α(a1 V), ε(a2 III)	2: β(a1 I), λ(a2 III), η(a2 II), δ(a3 IV)	3: γ(a1 I), γ(a3 IV), γ(a3 II)	4: δ(a1 I), β(a3 II); λ(a2 V), η(a2 IV)
5: ε(a2 I), α(a1 II), ε(a4 V), α(a1 VI)	6: η(a2 I), δ(a1 VI), β(a1 III); λ(a2 II)	7: κ(a2 I), κ(a2 II), κ(a2 III)	8: λ(a2 I), η(a2 III), δ(a1 V), β(a1 II)
9: α(a3 I), ε(a4 III), α(a3 V), ε(a4 IV)	10: β(a3 I), λ(a4 IV), η(a4 VI), δ(a1 III)	11: γ(a3 I), γ(a1 III), γ(a1 VI)	12: δ(a3 I), β(a1 VI); λ(a4 V), η(a4 III)
13: ε(a4 I), α(a3 VI), ε(a2 V), α(a3 II)	14: η(a4 I), δ(a3 II), β(a3 IV); λ(a4 VI)	15: κ(a4 I), κ(a4 IV), κ(a4 VI)	16: λ(a4 I), η(a4 IV), δ(a3 V), β(a3 VI)
17: γ(a1 II), γ(a1 V), γ(a3 III)	18: δ(a1 II), β(a3 III); λ(a2 VI), η(a2 V)	19: ε(a2 II), α(a1 III), ε(a4 VI), α(a3 IV)	20: ε(a4 II), α(a1 IV), ε(a2 VI), α(a3 III)
21: η(a4 II), δ(a3 III), β(a1 V); λ(a2 IV)	22: κ(a4 II), κ(a2 IV), κ(a2 V)	23: λ(a4 II), η(a2 V), δ(a3 VI), β(a1 IV)	24: κ(a4 III), κ(a4 V), κ(a2 VI)
25: λ(a4 III), η(a2 VI), δ(a1 IV), β(a3 V)	26: γ(a1 IV), γ(a3 VI), γ(a3 V)

Maximal entstehen 48 Flächen, dazu müssen die Flechtstreifen längs aller ihrer quer zum Streifen verlaufenden Viereckskanten und in jedem Viereck längs einer Diagonalen gefaltet werden.
Die Symmetriegruppe des Körpers enthält mindestens 12 Elemente, denn das Außenviereck a1 des Streifens I kann abgebildet werden auf die Außenvierecke a1 oder a3 jedes der 6 Streifen.
Durch geeignete Wahl der Längen b, c und d sowie der Winkel α, . . . , λ lassen sich Flechtstreifen für alle 5 Platonischen Körper sowie für das Kubo-Oktaeder, Deltoid-Ikosidodekaeder und das Disdyakis-Dodekaeder herstellen. Im Einzelnen:

Tetraeder
d = c = b = a
α = γ = ε = κ = 120^o
β = δ = η = λ = 60^o

Faltlinien:
die Pfeil-Diagonalen
von i2, a2, i4 und a4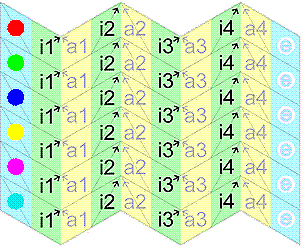

Schnittmuster
herunterladen: 2593 x 2105 Pixel, 315 kb: tr6.gif

zur Flechtseite ... wird fortgesetzt ... (letzte Aktualisierung: 27. Oktober 2007)