| Download of an
applet ("sympan.exe"), written in VB 5, expected to run under every | |
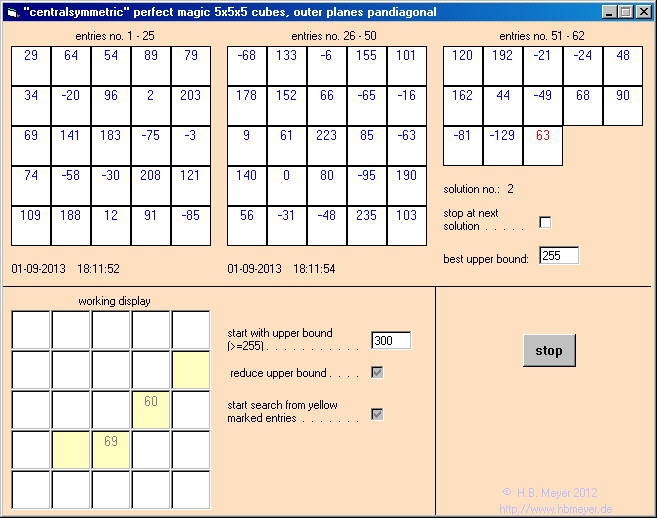 |
A perfect magic 5x5x5-cube consists of 125 integers, such that any 5 entries of any straight line and of any diagonal (spatial as well as plane) have sum 315. If, in addition, all 6 magic surface squares are pandiagonal (the broken diagonals sum up to 315, too), then the cube is a PMCP, a perfect magic cube with pandiagonal surface squares. A 5x5x5-cube is "centralsymmetric", if any two entries in position centralsymmetric to the cube midpoint, always have sum 126. In "Equations for perfect magic 5x5x5 cubes with pandiagonal surface squares" it has been proved, that every PMCP is "centralsymmetric". Such (non normal) PMCPs do exist and may be calculated with the program "sympan.exe" here. Due to symmetry, it is sufficent to show only the first 62 cube entries, the other 63 entries are c63= 63 and start with upper bound: user input of an upper bound n (255≤n) for the cube entries, the search for cube entries is restricted to integers from the interval [126-n,n]. reduce upper bound: when active: after producing a solution, the program searches for a solution with a smaller upper bound. yellow marked entries: the user may prescribe start values for c10, c14, c17, and c18 in the working display. start from yellow marked entries: when active: the search for cubes uses the yellow marked entries as start values. default values: when clicked: certain start values are written into the yellow marked fields. start: the search for the 5x5x5 magic cubes begins. stop: causes a break, the user is asked whether to continue or not. date and time are displayed when the computation starts and when the computation ends. the solution number and the last found solution are displayed. stop at next solution: causes a break, when the next solution is found. smallest upper bound: the smallest found integer n, such that all cube entries are contained in the interval [126-n,n]. |
| © H.B. Meyer Magic Squares and Cubes | |