Einträge c01,c02,...,c25
   
   
   
   
   
             
Einträge c26,c27,...,c50
   
   
   
   
   
             
Einträge c51,c52,...,c62
   
   
   
       
Summe:
ggT:  
 
01 02 03 04 05
06 07 08 09 10
11 12 13 14 15
16 17 18 19 20
21 22 23 24 25
 
 
26 27 28 29 30
31 32 33 34 35
36 37 38 39 40
41 42 43 44 45
46 47 48 49 50
 
         
51 52 53 54 55
  56 57 58 59 60  
  61 62 63 62 61
  60 59 58 57 56
  55 54 53 52 51
         
 
  25 24 23 22 21  
  50 49 48 47 46  
  51 52 53 54 55  
  26 27 28 29 30  
  01 02 03 04 05  
 
 
  20 19 18 17 16  
  45 44 43 42 41  
  56 57 58 59 60  
  31 32 33 34 35  
  06 07 08 09 10  
 
           
  15 14 13 12 11
  40 39 38 37 36  
  61 62 63 62 61  
  36 37 38 39 40  
  11 12 13 14 15  
           
         
  05 30 55 46 21  
  10 35 60 41 16  
  15 40 61 36 11  
  20 45 56 31 06  
  25 50 51 26 01  
         
         
  04 29 54 47 22  
  09 34 59 42 17  
  14 39 62 37 12  
  19 44 57 32 07  
  24 49 52 27 02  
         
             
  03 28 53 48 23  
  08 33 58 43 18  
  13 38 63 38 13  
  18 43 58 33 08  
  23 48 53 28 03  
             
Gleichungen für "zentralsymmetrische" perfekte magische 5x5x5-Würfel
erfordert JavaScript, © H.B. Meyer
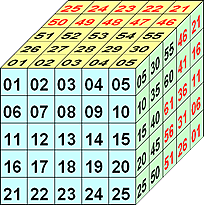Die 125 ganzzahligen Einträge eines 5x5x5-Würfels seien mit c01,c02,...,c125 bezeichnet. Die Nummerierung erfolgt von vorn nach hinten und in jedem zur Vorderseite parallelen 5x5-Quadrat von links oben nach rechts unten.
Nun seien alle 125 Plätze so mit ganzen Zahlen gefüllt, dass
1) die 5 Einträge auf jeder geraden Linie und jeder Diagonalen (räumlich oder eben) des Würfel stets die Summe 315 besitzen,
2) je zwei "antipodisch" gelegene Einträge (zentralsymmetrisch zum Würfelmittelpunkt c63 positioniert) zusammen 126 ergeben.
Dann sprechen wir von einem ZPMW, einem "zentralsymmetrischen" perfekten magischen Würfel. Da der mittlere Eintrag c63 die Zahl 63 sein muss, lässt sich ein ZPMW durch 62 Variable c01,...,c62 beschreiben, wie oben dargestellt. Die "Summme=315"- Bedingungen 1) eines ZPMW führen zu 42 (linear unabhängigen) Gleichungen, die durch Schaltknöpfe 1,...,42 (grün und rot) im "Kalkulator" links repräsentiert werden. Er startet mit der Gleichung 0 = 0. Anklicken eines grünen Schaltknopfs bewirkt Addition der zugeordneten Gleichung, rote Knöpfe bewirken Subtraktion. Werden z.B. die grünen Schaltknöpfe : 1, 2, 3, 4, und 5 und die roten: 6, 7, 8, 9 angeklickt, dann ergibt sich c05+c10+c15+c20+c25=315.
Mit dem "Kalkulator" lassen sich einige interessante Gleichungen für ZPMW-Einträge gewinnen: Durch Anklicken der grünen Schaltknöpfe: 1, 2, 4, 5, 36, 42 sowie der roten: 8, 10, 11, 37, 41, ergibt sich 2*c02+2*c10+2*c16+2*c24-3*c13=315.
Start und Anklicken von grün: 1, 2, 3, 4, 5, 12, 13, 14, 15, 16, 21, 36, 38 und rot: zweifach 6, 7, 8, 9, zweifach 17, 18, 19, 20, 22, 37, 39, 40 liefert das Ergebnis: -2*c06+2*c10-2*c46+2*c50+3*c61=189. Folglich muss c61 ungerade sein. Ähnlich erhält man die Gleichung -2*c17+2*c19-2*c27+2*c29+3*c62=189, die zeigt, dass c62 ebenfalls ungerade sein muss. Anklicken von grün: 10, 25, 29, 30, 35 und rot: 11, 27, 31, 33, 41, 42 liefert dieses Resultat.
Offensichtlich, ist 12*315+c61+c62 die Summe aller Einträge c01+c02+...+c62. Wegen der gleichen Parität von c61 und c62 muss dies eine gerade Zahl sein. Folglich ist die Anzahl der ungeraden Einträge unter den c01,c02,...,c62 eine gerade Zahl. Dies ergibt:
Satz  Ein "zentralsymmetrischer" perfekter magischer 5x5x5-Würfel kann nicht aus den Zahlen 1,2,...,125 bestehen.
Beweis   Wegen der Symmetrie, müssen genau 31 (eine ungerade Anzahl) der 62 Einträge c01,c02,...,c62 ungerade sein.
Bemerkung:  Anscheinend ist unbekannt, ob es einen ZPMW mit den Einträgen 0,2,3,...,124,126 (1,125 ersetzt durch 0,126) gibt.