entries c01,c02,...,c25
   
   
   
   
   
             
entries c26,c27,...,c50
   
   
   
   
   
             
entries c51,c52,...,c62
   
   
   
     
Sum:
gcd:
 
01 02 03 04 05
06 07 08 09 10
11 12 13 14 15
16 17 18 19 20
21 22 23 24 25
 
 
26 27 28 29 30
31 32 33 34 35
36 37 38 39 40
41 42 43 44 45
46 47 48 49 50
 
         
51 52 53 54 55
  56 57 58 59 60  
  61 62 63 62 61
  60 59 58 57 56
  55 54 53 52 51
         
 
  25 24 23 22 21  
  50 49 48 47 46  
  51 52 53 54 55  
  26 27 28 29 30  
  01 02 03 04 05  
 
 
  20 19 18 17 16  
  45 44 43 42 41  
  56 57 58 59 60  
  31 32 33 34 35  
  06 07 08 09 10  
 
           
  15 14 13 12 11
  40 39 38 37 36  
  61 62 63 62 61  
  36 37 38 39 40  
  11 12 13 14 15  
           
         
  05 30 55 46 21  
  10 35 60 41 16  
  15 40 61 36 11  
  20 45 56 31 06  
  25 50 51 26 01  
         
         
  04 29 54 47 22  
  09 34 59 42 17  
  14 39 62 37 12  
  19 44 57 32 07  
  24 49 52 27 02  
         
             
  03 28 53 48 23  
  08 33 58 43 18  
  13 38 63 38 13  
  18 43 58 33 08  
  23 48 53 28 03  
             
Equations for "centralsymmetric" perfect magic 5x5x5-cubes
JavaScript required, © H.B. Meyer

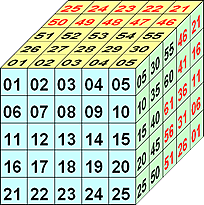
Let the 125 integer entries of a 5x5x5-cube be denoted by c01,c02,...,c125. Enumeration is done from front side to behind, and in every 5x5-square pane, parallel to the front pane, from left above to right below.
Now let all 125 places be filled with integer numbers such that
1) the 5 entries of any straight line, and any diagonal (spatial or plane), occuring in the cube, always have sum 315,
2) any "antipodal" pair of entries (in position centralsymmetric to the cube midpoint entry c63) has sum 126.
Then we speak of a CPMC, a "centralsymmetric" perfect magic cube. Since the middle entry c63 must be 63, the CPMC may be described by 62 variables c01,...,c62 as shown above. It turns out that the "sum=315" conditions 1) of a CPMC lead to 42 (linear independent) equations represented by buttons 1,...,42 (green and red) in the "calculator" at the left side. It starts with equation 0 = 0. Pressing a green button means addition of the attached equation, a red button causes subtraction. Pressing f.i. green buttons: 1, 2, 3, 4, and 5 and red buttons: 6, 7, 8, 9, one gets the equation c05+c10+c15+c20+c25=315.
Several interesting equations for CPMC-entries can be derived with the "calculator": by pressing green buttons: 1, 2, 4, 5, 36, 42 and red buttons: 8, 10, 11, 37, 41, one gets 2*c02+2*c10+2*c16+2*c24-3*c13=315.

Now start, press green buttons: 1, 2, 3, 4, 5, 12, 13, 14, 15, 16, 21, 36, 38 and red buttons: 2 times 6, 7, 8, 9, 2 times 17, 18, 19, 20, 22, 37, 39, 40. Result: -2*c06+2*c10-2*c46+2*c50+3*c61=189. Therefore c61 must be an odd integer. In a similar way the equation -2*c17+2*c19-2*c27+2*c29+3*c62=189, is obtained, showing that c62 has to be an odd integer, too. Press green buttons: 10, 25, 29, 30, 35 and red buttons: 11, 27, 31, 33, 41, 42 in order to get this result.
Obviously, the sum c01+c02+...+c62 of all 62 entries is 12*315+c61+c62. Due to the equal parity of c61 and c62 it must be an even integer. Hence the number of odd entries among the c01,c02,...,c62 must be even. This implies:
Theorem  A "centralsymmetric" perfect magic 5x5x5-cube cannot consist of the integers 1,2,...,125 exactly.
Proof         Due to symmetry, exactly 31 (an odd number) of the 62 entries c01,c02,...,c62 would have to be odd.
Remark:  It seems an open question, whether a CPMC can be built with entries 0,2,3,...,124,126 (1,125 replaced by 0,126).